数安实验6—鲁棒图像感知哈希

实验6：鲁棒图像感知哈希实验

1. 实验类别

        设计型实验：设计一种鲁棒性图像感知哈希算法，并给出实验结果。

2. 实验目的

        了解鲁棒性内容感知哈希技术的基本特点，设计并实现基于DCT的鲁棒性图像感知哈希。了解鲁棒性内容感知哈希技术在数字内容保护中的作用，掌握基于鲁棒性感知哈希的内容保护方法。

3. 实验条件

• WindowsXP或WindowsVista等操作系统
• Matlab 7.x以上版本软件
• 图像库

4. 实验原理

点击查看

4.1 原理

        数字图像的真实性完整性认证技术是多媒体安全保护的重要研究课题。图像完整性认证是不允许图像有任何丝毫的改变，在要求很严格或是非常机密的情况下就需要用到完整性认证。基于密码学意义上的认证方法均属于图像完整性认证。图像内容认证允许图像经受一些不损害图像质量的操作，只要使代表图像内容的特性得到认证即可。数字图像占据了数字化作品的很大一部分，除了数字图像本身的诸多优点外，数字图像还有如下特点：数据量大，在存储和传输的过程中会经受JPEG有损压缩、添加噪声、滤波等不会损耗图像内容质量的处理操作。这就要求我们在选择认证方法时不能选择完整性认证，而要选择内容性认证。在信息安全的发展过程中，基于图像内容认证的方法主要有数字水印和数字哈希两种方法。< br>         图像内容认证的两种方法里，数字水印的技术己日渐成熟，而数字哈希技术是一个新兴的课题，因此研究数字哈希技术更具有挑战性和实际意义。
       数字图像哈希是将图像数据映射到一个简短的固定长度的比特流中。根据人类视觉系统反应，使得不同内容的图像具有不同的哈希值，内容相似的图像具有相似的哈希值。

       现有的许多图像哈希方案都用以下三个步骤来产生哈希序列：

1. 产生一个关键依赖型的特征向量
2. 量化该特征向量
3. 压缩己经量化了的向量。

       其中最具有挑战性的一步就是第一步，产生的特征向量既要代表图像的内容，又要适应一些轻微的误差失真，如普通的过滤操作(如平均和均值滤波)、几何失真(如旋转，平移和尺度变换)、JPEG压缩和非线形亮度变化。其方法主要有：基于图像统计学特性的方法（灰度直方图、小波统计特性）、基于图像关系的方法（DCT系数对、小波系数对）、基于原始图像特征表述的方法（SVD值）、基于低层图像特征提取的方法（特征点）等等。

4.2 典型应用

        图像哈希的典型应用是相似图像搜索。如Google和Tineye相似图像搜索主要利用的算法是感知哈希算法，它的作用是对每张图片生成一个“指纹”字符串，然后比较不同图片的指纹，结果越接近，就说明图片越相似。典型算法有：
        1. ahash算法

• 缩小尺寸：将图片缩小到8x8的尺寸，总共64个像素。去除图片的细节，只保留结构、明暗等基本信息，摒弃不同尺寸、比例带来的图片差异。
• 简化色彩：将缩小后的图片，转为64级灰度。也就是说，所有像素点总共只有64种颜色。
• 计算平均值：计算所有64个像素的灰度平均值。
• 比较像素的灰度：将每个像素的灰度，与平均值进行比较。大于或等于平均值，记为1；小于平均值，记为0。
• 计算哈希值：将上一步的比较结果，组合在一起，这就是这张图片的指纹。
• 计算“汉明距离”，如果不相同的数据位不超过某个阈值，就说明两张图片很相似，距离为0说明完全相同；如果大于某个阈值，就说明这是两张不同的图片。

        2. phash算法

• 图片缩放：缩小尺寸到 32×32
• 图像灰度化：转化为256灰度图
• 对图像进行DCT变换
• 缩小DCT：DCT是32*32，保留左上角的8*8，代表图片的低频区域
• 计算平均值：计算缩小DCT后的所有像素点的平均值
• 与均值比较：将每个像素的DCT值，与平均值进行比较。大于或等于平均值，记为1；小于平均值，记为0。
• 计算哈希值：将上一步的比较结果，组合在一起，这就是这张图片的指纹。
• 用汉明距离比较：如果不相同的数据位不超过某个阈值，就说明两张图片很相似，距离为0说明完全相同；如果大于某个阈值，就说明这是两张不同的图片。

        3. dhash算法

• 缩小图片：收缩到8*8的大小，共有72个像素点
• 转化为灰度图：转化为256灰度图
• 计算差异值：dHash算法工作在相邻像素之间，这样每行9个像素之间产生了8个不同的差异，一共8行，则产生了64个差异值
• 获得指纹：如果左边的像素比右边的更亮，则记录为1，否则为0
• 用汉明距离比较：如果不相同的数据位不超过某个阈值，就说明两张图片很相似，距离为0说明完全相同；如果大于某个阈值，就说明这是两张不同的图片。

        4. whash算法

• 缩小图片：缩小尺寸到 32×32
• 转化为灰度图：转化为256灰度图
• 对图像进行DWT变换,取低频信息
• 对图像进行DWT变换,取低频信息
• 与均值比较：将低频区域的每个像素点的DWT值，与平均值进行比较。大于或等于平均值，记为1；小于平均值，记为0。
• 计算哈希值：将上一步的比较结果，组合在一起，这就是这张图片的指纹。
• 用汉明距离比较：如果不相同的数据位不超过某个阈值，就说明两张图片很相似，距离为0说明完全相同；如果大于某个阈值，就说明这是两张不同的图片。

4.3 算法实现

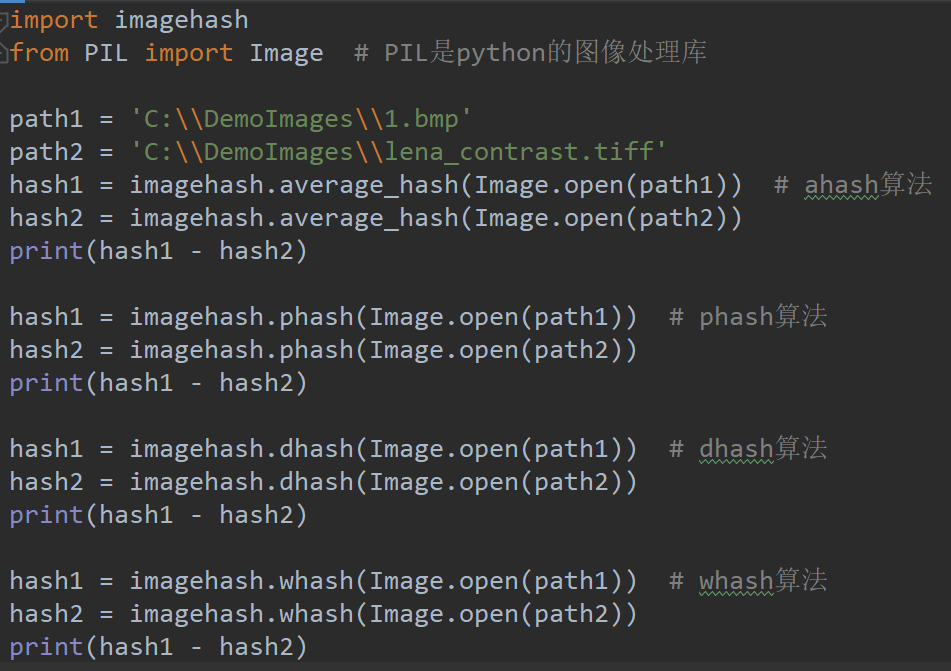
        Python的imagehash库（https://github.com/JohannesBuchner/ imagehash）实现了上述四种算法，具体过程如下：

1. 安装imagehash库，pip install imagehash
2. 调用相应的哈希函数

5. 实验要求

        本实验实现一种基于视觉特性的图像感知哈希算法，可通过密钥控制哈希序列，保证安全性，具体过程如下：

1. 读入两幅图像，对图像做预处理：如果读入的是彩色图像，将其转换为灰度图像rgb2gray；在灰度图像中利用差值方式将图像重采样为64×64的标准化图表示imresize

2. 对标准化图像进行8×8子块划分，将标准化图像划分为$\frac{6464}{（88）}=64$个子块，依次对各子块进行二维离散余弦变换dct2

   fun = @dct2
   Ic = blkproc(I,[8 8],fun)

   并依次将各分块的DC系数，即（1,1）置为0；

3. 生成N 个64×64伪随机矩阵：首先通过密钥伪随机生成服从标准正态的64×64矩阵randn('state',key)，randn，然后用高斯低通滤波器进行迭代滤波K=fspecial('gaussian'); Y=filter2(K,Y);

   

4. 设DCT敏感度矩阵m

   $$m = \left [ \begin{matrix} 71.43 & 99.01 & 86.21 & 60.24 & 41.67 & 29.16 & 20.88 & 15.24 \\ 99.01 & 68.97 & 75.76 & 65.79 & 50.00 & 36.90 & 27.25 & 20.28 \\ 86.21 & 75.76 & 44.64 & 38.61 & 33.56 & 27.47 & 21.74 & 17.01 \\ 60.24 & 65.79 & 38.61 & 26.53 & 21.98 & 18.87 & 15.92 & 13.16 \\ 41.67 & 50.00 & 33.56 & 21.98 & 16.26 & 13.14 & 11.48 & 9.83 \\ 29.16 & 36.90 & 27.47 & 18.87 & 13.14 & 10.40 & 8.64 & 7.40 \\ 20.88 & 27.25 & 21.74 & 15.92 & 11.48 & 8.64 & 6.90 & 5.78 \\ 15.24 & 20.28 & 17.01 & 13.16 & 9.83 & 7.40 & 5.78 & 4.73 \end{matrix} \right ]$$

   对矩阵m进行周期延拓得到大小为64 ×64 的矩阵M ,并将其每个元素作为Ic的对应位置频率系数在特征值计算中的权。

5. 取第一个伪随机矩阵，计算:

   $$Y_n = \sum_{i=1}^{s_1}\sum_{j=1}^{s_2}[I_c(i,j)·P_n(i,j)·M(i,j)]$$

   如果$Y_N <0$，则$H(n)=0$，反之则$H(n)=1$；

6. 循环第5步，直到将所有的N 个64×64伪随机矩阵都计算完，最终生成一个N比特的Hash向量

7. 比较两幅图像hash向量的汉明距离dis，设定一个合适的阈值tau，如果dis<tau，则两幅图像内容一致；反之则是内容不同的两幅图像。汉明距离为:

   $$dis = \frac{norm(hashVec1-hashVec2)}{2×\sqrt{norm(hashVec1)*norm(hashVec2)}}$$

   以上步骤的程序：

   • 两个图片的比较

     clc;clear;
     key = 1;
     tau = 0.225; 
     Hashlen = 1000;
     
     I1 = imread('HashingToolbox/DemoImages/1.bmp');
     I2 = imread('C:\Users\86159\Desktop\学习\4-数字内容安全实验\实验六\HashingToolbox\DemoImages\lena_color.jpg');
     % 读取两幅图片，并转为灰度图像
     I1 = im2gray(I1); 
     I2 = im2gray(I2);
     % 对图片重采样为64*64的标准化图
     I1 = imresize(I1,[64,64]);
     I2 = imresize(I2,[64,64]);
     % 将图片划分成8*8子块，并进行二维离散余弦变换
     fun = @dct2;
     I1 = blkproc(I1,[8 8],fun);
     I2 = blkproc(I2,[8 8],fun);
     % 分块的DC系数，即（1,1）置为0
     I1(1,1) = 0;
     I2(1,1) = 0;
     % 通过密钥伪随机生成Hashlen个服从标准正态64*64矩阵
     randn('state',key);
     N = cell(1,Hashlen);
     % 用高斯低通滤波器进行迭代滤波
     K = fspecial('gaussian');
     Y = cell(1,Hashlen);
     
     for i = 1:Hashlen
         N{i} = randn(64);
         Y{i} = filter2(K,N{i});
     end
     % DCT敏感度矩阵m,周期延拓至64*64
     m = [
     71.43 99.01 86.21 60.24 41.67 29.16 20.88 15.24;
     99.01 68.97 75.76 65.79 50.00 36.90 27.25 20.28;
     86.21 75.76 44.64 38.61 33.56 27.47 21.74 17.01;
     60.24 65.79 38.61 26.53 21.98 18.87 15.92 13.16;
     41.67 50.00 33.56 21.98 16.26 13.14 11.48 9.83;
     29.16 36.90 27.47 18.87 13.14 10.40 8.64 7.40;
     20.88 27.25 21.74 15.92 11.48 8.64 6.90 5.78;
     15.24 20.28 17.01 13.16 9.83 7.40 5.78 4.73];
     % 矩阵m进行周期延拓得到大小为64 ×64 的矩阵M
     M = repmat(m,8,8);
     I1_Hash = ones(1,Hashlen);
     I2_Hash = ones(1,Hashlen);
     % 对Hashlen个伪随机矩阵遍历计算
     for k = 1:Hashlen
         I1_sum = 0;
         I2_sum = 0;
         for i = 1:64
             for j = 1:64
                 I1_sum = I1_sum + I1(i,j) * Y{k}(i,j) * M(i,j);
                 I2_sum = I2_sum + I2(i,j) * Y{k}(i,j) * M(i,j);
             end
         end
         if I1_sum < 0
             I1_Hash(k) = 0;
         end
         if I2_sum < 0
             I2_Hash(k) = 0;
         end
     end
     % 汉明距离
     dis = norm((I1_Hash-I2_Hash)/2*sqrt(norm(I1_Hash)*norm(I2_Hash)));
     % 与阈值比较
     if tau < dis
         ds = '不相似';
         zo = 0;
     else
         ds = '相似';
         zo = 1;
     end
     disp(ds)

   • 以1.bmp为基准图，与DemoImages文件中其他图片对比：

     封装成函数：

     function[ds] = imgHashSimilar(I1,I2,tau,key,Hashlen)
     % 读取两幅图片，并转为灰度图像
     I1 = im2gray(I1); 
     I2 = im2gray(I2);
     % 对图片重采样为64*64的标准化图
     I1 = imresize(I1,[64,64]);
     I2 = imresize(I2,[64,64]);
     % 将图片划分成8*8子块，并进行二维离散余弦变换
     fun = @dct2;
     I1 = blkproc(I1,[8 8],fun);
     I2 = blkproc(I2,[8 8],fun);
     % 分块的DC系数，即（1,1）置为0
     I1(1,1) = 0;
     I2(1,1) = 0;
     % 通过密钥伪随机生成Hashlen个服从标准正态64*64矩阵
     randn('state',key);
     N = cell(1,Hashlen);
     % 用高斯低通滤波器进行迭代滤波
     K = fspecial('gaussian');
     Y = cell(1,Hashlen);
     
     for i = 1:Hashlen
         N{i} = randn(64);
         Y{i} = filter2(K,N{i});
     end
     % DCT敏感度矩阵m,周期延拓至64*64
     m = [
     71.43 99.01 86.21 60.24 41.67 29.16 20.88 15.24;
     99.01 68.97 75.76 65.79 50.00 36.90 27.25 20.28;
     86.21 75.76 44.64 38.61 33.56 27.47 21.74 17.01;
     60.24 65.79 38.61 26.53 21.98 18.87 15.92 13.16;
     41.67 50.00 33.56 21.98 16.26 13.14 11.48 9.83;
     29.16 36.90 27.47 18.87 13.14 10.40 8.64 7.40;
     20.88 27.25 21.74 15.92 11.48 8.64 6.90 5.78;
     15.24 20.28 17.01 13.16 9.83 7.40 5.78 4.73];
     % 矩阵m进行周期延拓得到大小为64 ×64 的矩阵M
     M = repmat(m,8,8);
     I1_Hash = ones(1,Hashlen);
     I2_Hash = ones(1,Hashlen);
     % 对Hashlen个伪随机矩阵遍历计算
     for k = 1:Hashlen
         I1_sum = 0;
         I2_sum = 0;
         for i = 1:64
             for j = 1:64
                 I1_sum = I1_sum + I1(i,j) * Y{k}(i,j) * M(i,j);
                 I2_sum = I2_sum + I2(i,j) * Y{k}(i,j) * M(i,j);
             end
         end
         if I1_sum < 0
             I1_Hash(k) = 0;
         end
         if I2_sum < 0
             I2_Hash(k) = 0;
         end
     end
     % 汉明距离
     dis = norm((I1_Hash-I2_Hash)/(2*sqrt(norm(I1_Hash)*norm(I2_Hash))));
     % 与阈值比较
     if tau < dis
         ds = '不相似';
     else
         ds = '相似';
     end

     新建一个.m文件，循环调用函数，进行多个图片比较：

     clc;clear;
     figure('NumberTitle', 'off', 'Name', '图片相似度比较');
     key = 1;
     tau = 0.225;
     Hashlen = 1000;
     
     % 获取DemoImages中全部图片路径
     img_path = dir('HashingToolbox/DemoImages/*');
     img_path = img_path(~[img_path.isdir]);
     fileList = fullfile({img_path.folder}.', {img_path.name}.');
     
     I1 = imread('HashingToolbox/DemoImages/1.bmp');
     subplot(4,ceil(length(fileList)/4),1);imshow(I1);title('基准图');
     for i = 2:length(fileList)
         I2 = imread(fileList{i});
         ds = imgHashSimilar(I1,I2,tau,key,Hashlen);
         disp(fileList{i})
         subplot(4,ceil(length(fileList)/4),i);imshow(I2);title(ds);
     end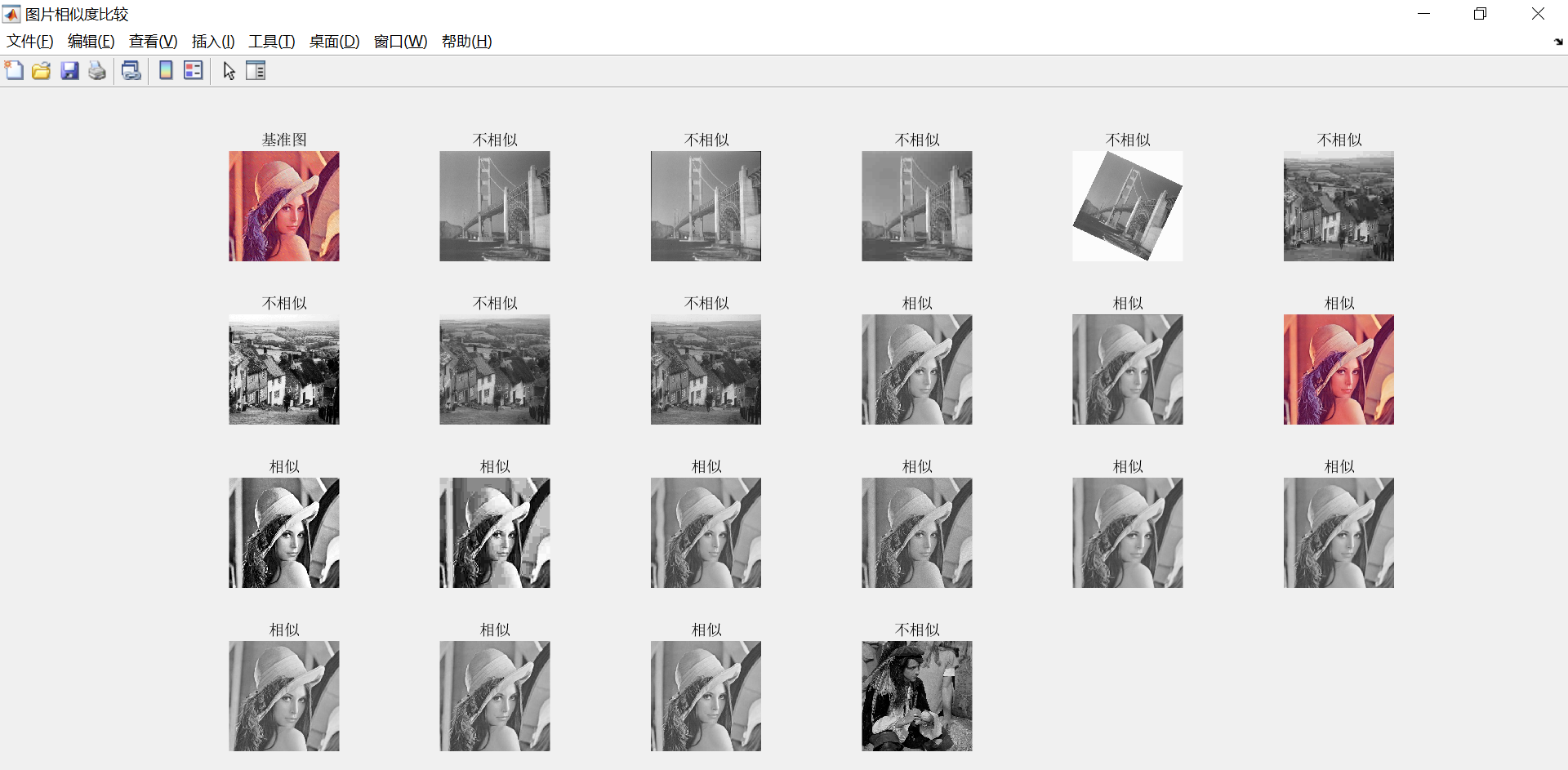

     

8. 关于实验报告

   1. 关于tau的选取，tau是一个经验值，其选取依据是根据测试集的准确率决定，给出选取过程。

      通过控制变量：N=1000，key=1的情况下：

      

   2. 关于N的选取，N 值越大Hash精度越高,与不同图像Hash碰撞的概率就越小,但鲁棒性会降低,因而需设定合适的N值，以满足Hash在精度和鲁棒性之间的折衷，给出选取过程。

             当Hash的位数决定了其能够表示不同图形的个数，即最大为$2^n$个。通过实验可以测得在tau和key不变的情况下，Hash的位数越大图像感知越精密，图片相似度判断越精准，但意味着计算机容错降低，并且算出的汉明距离变小，从而更需要tau训练出更加精准判别的阈值，提高了训练成本。因此我认为折衷方案应为根据图片数量N取较大于$2^n$中n的数值。

6. 可选实验

1. 关于key，验证密钥的安全性。

           根据实验中测试，改变key的值会极大影响tau阈值的范围。实验中选择的key=1，显然不具有安全性，可以采用一次一密的伪随机数生成器来进行密钥选取，从而提高其安全性。

2. 试设想图像感知哈希的应用场景，请设计一种应用场景。

           在图片版权争议问题上，可以通过图像感知哈希判断图片相似度，从而判定是否侵权。

7. 实验中出现的问题

• 在读取12.tif时报错称需要MN3格式，即RGB格式。这是因为该图片深度为32位，应通过软件将其改为24位
• 在用matlab函数读取图片集的样本时，发现多出一个看不见的Thumbs.db，这是系统的缩略图缓存文件，只要在设置里面关闭即可。Win10如何删除thumbs.db

鸣谢❀参考大佬文章

• 秦玉辉的实验报告