现代密码教程—分组密码
现代密码学教程—分组密码
作业(尚未订正)
第二节:
证明
3DES的穷举攻击复杂度为:$Time=2^{112}, space ≈ 2^{56}$。以
DES-EEE3为标准时,加密K1-加密K2-加密K3,密钥总长度为168 bit,利用中途相遇攻击,将明文穷举两次加密后存储,共占$space ≈ 2^{56}$,密文穷举解密后与存储相对应,对应上则可确定K1,K2,K3,其计算复杂度为$Time=2^{112}$。以
DES-EEE2为标准,加密K1-加密K2-加密K1,密钥总长度为112 bits,虽然第一次和第二次加密使用相同的密钥,但是在穷举攻击时并不能最先确定出其密钥,因此普通的穷举攻击和中途相遇攻击均需要计算复杂度为$Time=2^{112},space ≈ 2^{56}$。如果16轮使用的子密钥$K{16} = K_1,K{15}=K_2,…, K_9=K_8$,则加密所用的子密钥与解密所用的子密钥相同,对一个明文X加密两次,得到的还是明文X。弱密钥的定义:若k使得加密函数与解密函数一致,则称k为弱密钥。证明下列密钥为弱密钥(偶校验:就是让原有数据序列中(包括你要加上的一位)1的个数为偶数):
(1)
0x00000000000000加入偶校验位后为
0x0000000000000000,C,D存数编号(00,00),其中56位有效密钥全为0,在通过密钥编排时,无论密钥如何移位得到的子密钥均为0,从而使得在F函数中使用密钥加无任何意义,因此该密钥为弱密钥。(2)
0x1E1E1E1E0F0F0F0F写成二进制形式,通过
PC-1置换后,C,D存数编号(00,11),即得到的C中元素全部为0,得到的D中元素全部为1,从而所有的子密钥相同,并且 DES 是 Feistel 网络的结构,因此其为弱密钥。(3)
0xE1E1E1E1F0F0F0F0同(2)写成二进制形式,通过
PC-1置换后,C,D存数编号(11,00),即得到的C中元素全部为1,得到的D中元素全部为0,从而所有的子密钥相同,并且 DES 是 Feistel 网络的结构,因此其为弱密钥。(4)
0xFFFFFFFFFFFFFF同(1),C,D存数编号(11,11),因此子密钥均为1,使得在F函数中使用密钥加无任何意义,因此该密钥为弱密钥。
第三节:
尝试推导
AES的列混合操作转化为矩阵乘法$b(x)=a(x)*c(x) mod(x^4+1),c(x)= 03x^3+01x^2+01x+02$列混合的定义为:将状态矩阵的每一列看成$GF(2^8)$上的多项式,并和一个固定的多项式$c(x)=03x^3+01x^2+01x+02$相乘再模$x^4+1$。例如:对于状态矩阵的某一列$\begin{bmatrix}a_0 & a_1 & a_2 & a_3\end{bmatrix}^T$看为$a(x)=a_3x^3+a_2x^2+a_1x+a_0$,从而列混合可表示为:$a(x)*c(x) mod(x^4+1)$。
对于任意$x^i$,有$x^imod(x^4+1)=x^{i(mod4)}$,因此可以在计算多项式相乘再取模的结果时进行简化,例如:$x^6=x^2,x^5=x,x^4=1$。
上述公式表达的即为题中所示的矩阵乘法。
快速计算法,计算
0x87乘以0x03模$m(x)=x^8+x^4+x^3+x+1$的值。调研
SM4算法,其迭代结构属于何类型?并详细描述加解密及密钥编排的步骤。SM4算法是一种分组密码算法。其分组长度为128bit,密钥长度也为128bit。加密算法与密钥扩展算法均采用32轮非线性迭代结构,以字(32位)为单位进行加密运算,每一次迭代运算均为一轮变换函数F。SM4算法加/解密算法的结构相同,只是使用轮密钥相反,其中解密轮密钥是加密轮密钥的逆序。
加/解密:
算法由32次迭代算法和1次反序变换R组成。设明文输入为$(X_0,X_1,X_2,X_3)\in(Z_2^{32})^4$,密文输出为$(Y_0,Y_1,Y_2,Y_3)\in(Z_2^{32})^4$,轮密钥为$rk_i\in Z_2^{32},i=0,1,2,…,31$。加密运算过程为:
32次迭代运算:$X{i+4}=F(X_i,X{i+1},X{i+2},X{i+3},rk_i),i=0,1,2,…,31$
反序变换:$(Y0,Y_1,Y_2,Y_3)=R(X{32},X{33},X{34},X{35})=(X{35},X{34},X{33},X_{32})$
迭代运算中轮函数F:
设输入为$(X0,X_1,X_2,X_3)\in(Z_2^{32})^4$,轮密钥为$rk_i\in Z_2^{32},i=0,1,2,…,31$,则轮函数F为:$F(X_0,X{1},X{2},X{3},rk_i)=X_0\oplus T(X_1 \oplus X_2 \oplus X_3 \oplus rk)$。
轮函数F中合成置换T:
T:$Z^{32}_2→Z^{32}_2$是一个可逆变换,由非线性变换τ和线性变换L复合而成,即T(.)=L(τ(.))。非线性变换τ由4个并行的S盒构成。设输入为$A=(a_0,a_1,a_2,a_3)∈(Z^8_2)^4$,输出为$B=(b_0,b_1,b_2,b_3)∈(Z^8_2)^4$,则:$(b_0,b_1,b_2,b_3)=τ(A)=(Sbox(a_0),Sbox(a_1),Sbox(a_2),Sbox(a_3))$。Sbox为固定的16进制置换表。
合成置换T中线性置换L
非线性变换τ的输出是线性变换L的输入.设输入为$B∈Z^{32}_2$,输出为$C∈Z^{32}_2$,则:$C=L(B)=B \oplus (B<<<2) \oplus (B<<<10) \oplus (B<<<18) \oplus(B<<<24)$
解密时只是将轮密钥的使用顺序进行逆向进行。
密钥编排:
已知加密密钥为$MK=(MK0,MK_1,MK_2.MK_3)$,系统参数$FK=(FK_0,FK_1,FK_2,FK_3)$,固定参数$CK=(CK_0,CK_1,…,CK{31})$。$rk_i$为轮密钥,轮密钥由加密密钥生成。
首先:$(K0,K_1,K_2,K_3)=(MK_0 \oplus FK_0,MK_1 \oplus FK_1,MK_2 \oplus FK_2,MK_3 \oplus FK_3)$对$i=0,1,2,…,31$:$rk_i=K{i+4} \oplus T’(K{i+1} \oplus K{i+2} \oplus K_{i+3} \oplus CK_i)$,改变换与加密中的T变换基本相同,只是将其中的线性变换改为:$L(B)=B \oplus (B<<13) \oplus (B<<23)$,由于系统参数个固定参数是已知的,轮密钥即可求得。
(选作)使用乘法逆元及仿射方法实现
AES字节代换操作的快速运算方法。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91# S盒乘法逆元及仿射实现
# 求最高幂次数
def Nonzero_MSB(value):
v2str = '{:09b}'.format(value)
for i in range(9):
if int(v2str[i]):
return 9 - i
# 模2除法:m为被除数。b为除数,q为商,r为余数
def Mode2_div(fx, gx):
n = Nonzero_MSB(fx)
m = Nonzero_MSB(gx)
if n < m:
return [0, fx]
deg = n - m
fx = fx ^ (gx << deg)
[q, r] = Mode2_div(fx, gx)
return [(1 << deg) | q, r]
# 多项式乘法
# v3 = v1 - q3 * v2
def Calculate(v1, q3, v2):
value = 0
for i in range(32):
if (q3 & (1 << i)):
value = value ^ (v2 << i)
return v1 ^ value
# 欧几里得算法
def poly_gcd(r1, r2, v1=1, v2=0, w1=0, w2=1):
if r2 == 0 or r2 == 1:
return w2
q3, r3 = Mode2_div(r1, r2) # q3(x)=r1(x)|r2(x), r2(x)=r1(x) mod r2(x)
v3 = Calculate(v1, q3, v2) # v3 = v1 - q3 * v2
w3 = Calculate(w1, q3, w2) # w3 = w1 - q3 * w2
return poly_gcd(r2, r3, v2, v3, w2, w3)
def sym2int(sym):
power = [sym[i + 2] for i in range(len(sym)) if sym[i] == 'x']
if '+1' in sym: power.append('0')
data = 0
for p in power:
data = data | (1 << int(p))
return data
def int2sym(data):
int2str = '{:09b}'.format(data)
sym = ''
for i in range(9):
if int(int2str[i]) == 1:
if 8 - i:
sym += '+x^%d' % (8 - i)
else:
sym += '+1'
return sym[1:]
def xor(a, b):
if a == b:
return '0'
else:
return '1'
def fangshe(a):
a = a[::-1]
c = '11000110'
b = ''
for i in range(7, -1, -1):
b += xor(xor(xor(xor(xor(a[i], a[(i + 4) % 8]), a[(i + 5) % 8]), a[(i + 6) % 8]), a[(i + 7) % 8]), c[i])
return b
if __name__ == '__main__':
bi = bin(int(input('请输入两位16进制数:'), 16))[2:]
print("16进制转为为2进制为:{}".format(bi))
xstr = ''
for i in range(len(bi)):
if bi[i] == '1':
if i < len(bi) - 1:
xstr += "+x^{}".format(len(bi) - i - 1)
elif i == str(len(bi)):
xstr += '+1'
xstr = xstr[1:]
inverse = int2sym(poly_gcd(283, sym2int(xstr)))
data = hex(sym2int(inverse))
print('你输入的多项式 :', xstr)
print('默认既约多项式 :', int2sym(283))
print('乘法逆元为 :', inverse)
print('乘法逆元的16进制:', data)
print('---- 多项式乘法逆元求解完成 ----')
data = bin(int(data, 16))[2:].zfill(8)
print('最终结果为:', fangshe(data))
print('16进制表示为', hex(int(fangshe(data), 2)))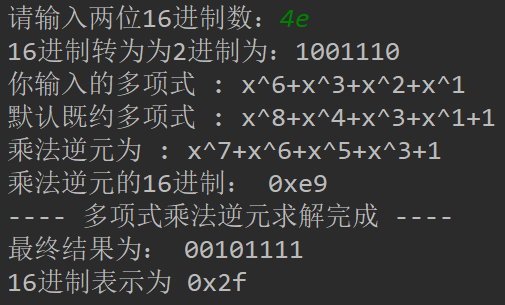
第四节:
调研
OFB模式及CCM模式,并分析其各自性质。OFB模式(输出反馈模式):密码算法的输出会反馈到密码算法的输入当中。其是将“明文分组”和“密码算法的输出”进行XOR来产生“密文分组”。优点:传输过程中密文在某位上发生的错误不会影响解密后明文其他位。缺点:失去同步,如果加密端和解密端移位寄存器不同步,那么恢复的明文将是一些无用的杂乱数据,任何使用OFB的系统必须有检测失步的机制,并用新的初始向量IV填充双方移位寄存器重新获得同步;抗消息流篡改攻击能力不如CFB。CCM模式(认证保密模式):CCM是CTR加密模式和CMAC认证算法的混合使用,常用在需要同时加密和认证的领域,比如WiFi安全中的WPE协议,它就使用了AES-CCM模式。其首先使用CBC-MAC模式来认证传输帧,然后使用CTR模式来加密帧。


